Improving RTKLIB solution: (AR lock count and elevation mask)

In the previous post, after a couple changes to the input parameters, we ended up with the following solution for the difference between two stationary, then moving Ublox receivers:

During the time when the receivers were stationary (17:25 to 17:45), we were able to hold a fixed solution (green in plot) continuously after the initial convergence, but started to revert to float solution (yellow in plot) fairly frequently once the receivers started moving.

Let's look at the data a little closer to see if we can discern why we are reverting back to the float solution. If we switch to the “Nsat” view in RTKPLOT plotted below, we can see a couple of useful plots.

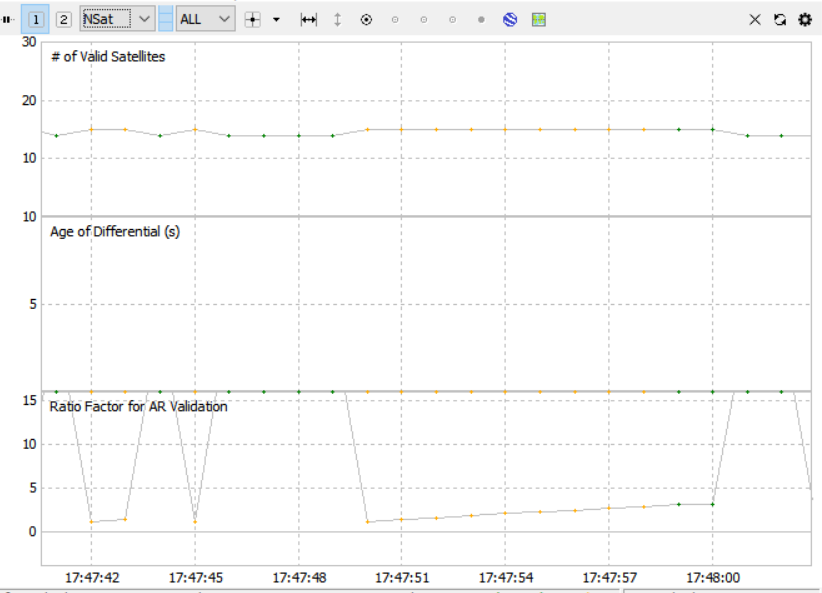
The top plot shows the number of satellites used for the solution and the bottom plot show the AR ratio factor. The AR ratio factor is the residuals ratio between the best solution and the second best solution while attempting to resolve the integer cycle ambiguities in the carrier-phase data. In general, the larger this number, the higher confidence we have in the fixed solution. If the AR ratio exceeds a set threshold, then the fixed solution is used, otherwise the float solution is used. I have left this threshold at its default value of 3.0.

Notice in the plot that each time we revert to the fixed solution, it happens when the number of valid satellites increases. At first this seems counter-intuitive, you would think that more information would improve the solution, not degrade it. What is happening though, is that the solution is not using the satellite data directly, but rather, the kalman filter estimate of the data. This estimate improves as the number of samples increases. This is also why the solution takes some time to converge at the beginning of the data. By using the data from the new satellite before the kalman filter has had time to converge, we are adding large errors to the solution, forcing us back to the float solution.

Fortunately, RTKLIB has a parameter in the input configuration file to address this issue. “Pos2-arlockcnt” sets the minimum lock count which has to be exceeded before using a satellite for integer ambiguity resolution. This value defaults to zero, but let's change it to 20 and see what happens. While we are it, we will also change the related parameter “pos2-arelmask” which excludes satellites with elevations lower than this number from being used. We will change this from it's default of 0 to 15 degrees.

Unfortunately, re-running the solution with these changes makes almost no difference as seen below. The jumps back to float solutions still occur immediately after a new satellite is included, and the additional satellites are being included at the same epochs. Something is clearly wrong.

Digging into the code a bit reveals the problem. First, the arlockcnt input parameter is copied to a variable called “rtk->opt.minlock” Then the relevant lines of code from rtkpos.c are:

rtk->ssat[sat[i]-1].lock[f]=-rtk->opt.minlock;

if (rtk->ssat[i-k].lock[f]>0&&!(rtk->ssat[i-k].slip[f]&2)&&
     rtk->ssat[i-k].azel[1]>=rtk->opt.elmaskar) {
     rtk->ssat[i-k].fix[f]=2; /* fix */
     break;
}
else rtk->ssat[i-k].fix[f]=1;

So far, everything looks OK, but when we look at the definition for the structure member “lock” in rtklib.h we find:

unsigned int lock [NFREQ]; /* lock counter of phase */

This won't work. We are assigning a negative number (-rtk->opt.minlock) to an unsigned variable, then checking if the unsigned variable is greater than zero, which by definition, will always be true. Hence, satellites are always used immediately, regardless of lock count.

We fix this bug by changing the definition of lock from unsigned to signed:

int lock [NFREQ]; /* lock counter of phase */

Rerunning after rebuilding the code, gives us the following solution:

Much better! All but a couple of the jumps back to float solutions have been eliminated.

Looking at the plot of the AR ratio for this solution, we can see that the kalman filter requires more than 20 seconds (the value we chose for arlockcnt) to re-converge. Two minutes looks like a more reasonable value from the plot, so let's try rerunning the solution with arlockcnt=120.

Even better.  That eliminates the last couple of jumps back to the float solution and also significantly reduces the number of jumps in the AR ratio plot as shown below. The green line in the bottom plot is arlockcnt=20 and the blue line is arlockcnt=120.

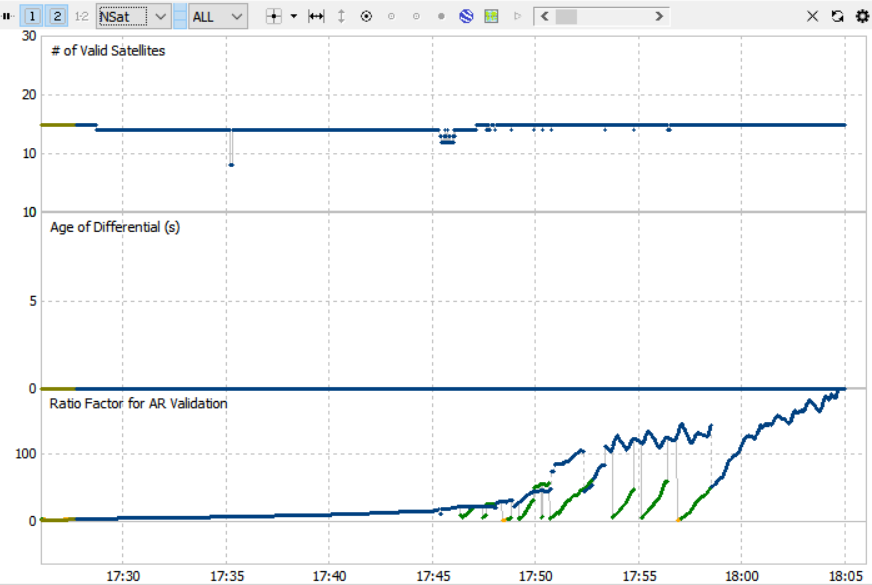
It's possible we will need to revisit this number after looking at more data, but for now we will use 120 secs.

As always, please leave a comment if you have any comments, discussion points, or questions.

Update 4/11/16:  

• In the above discussion, my data is one epoch/sec and I equate epochs with seconds.  Arlockcnt is specified in epochs, not seconds, so if your data is at a different sample rate you will need to adjust accordingly.
• The suggestion above to set arlock to 120 secs is probably too conservative for more challenging environments.  If there are few satellites and/or many cycle slips for example it is probably better to start using a just-locked satellite before it is fully converged.  I have started using 30 secs rather than 120 secs for my solutions.
• You can pull this code fix from my github repository either by itself from the arlockcnt branch or as part of a larger set in the demo1 branch